Назначение и ключевые особенности программного обеспечения
На данном веб-сайте представлены программные средства мультимедийного обучения на основе современных технологий компьютерной графики и имитационно-численного моделирования.
Основное назначение программных продуктов: симуляционное выполнение лабораторных работ, моделирование физических процессов, наглядная демонстрация принципов работы устройств, отработка навыков управления различным оборудованием.
Реалистичность визуального ряда

Представленные симуляционные модели отличаются реалистичной графической визуализацией объекта исследования в реальном времени по средствам современной игровой 3D-графики. К графической составляющей программных продуктов предъявляются особые требования, соответствующие мировому уровню развития технологии компьютерной графики. Прототипы применяемых трехмерных моделей разрабатываются в детальном соответствии с реальным оборудованием, а для динамической прорисовки объектов виртуального трёхмерного пространства используется шейдерная технология, что позволяет добиваться высокого качества изображения в отношении прорисовки фактуры материалов, динамического освещения и построения теней.
Высокая интерактивность
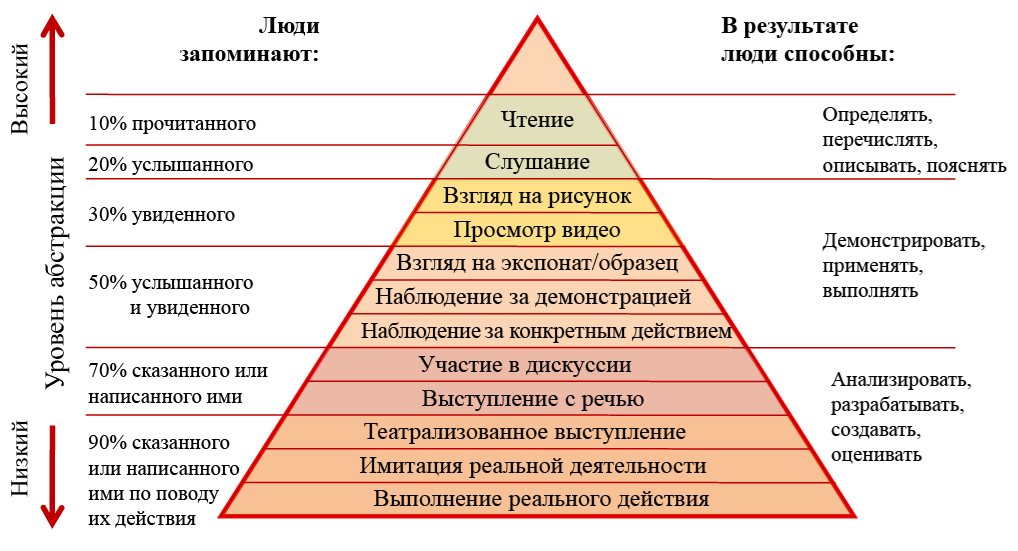
Вопросу взаимодействия пользователя с элементами виртуального трёхмерного окружения уделяется особое внимание. Поскольку основной задачей программных продуктов является интенсивное влияние на развитие когнитивной функции пользователя в отношении конкретного предмета исследования, то необходимо максимально снизить уровень абстракции предлагаемого учебного контента, а, следовательно, увеличить степень свободы действий пользователя в виртуальном трёхмерном пространстве. Необходимым условием здесь является возможность выполнения «ошибочных» действий учащимся и адекватное реагирование имитационной модели на эти действия с целью достижения требуемого уровня понимания учебного материала учащимся.
Информационно-методическое сопровождение
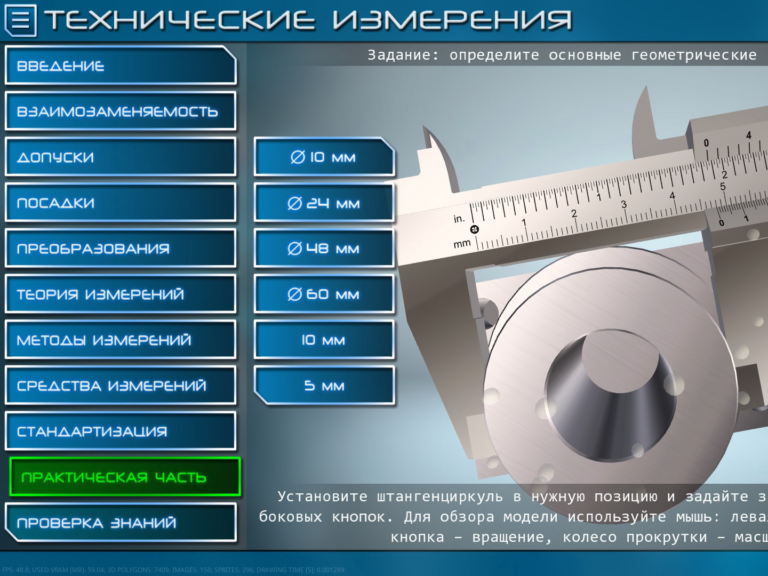
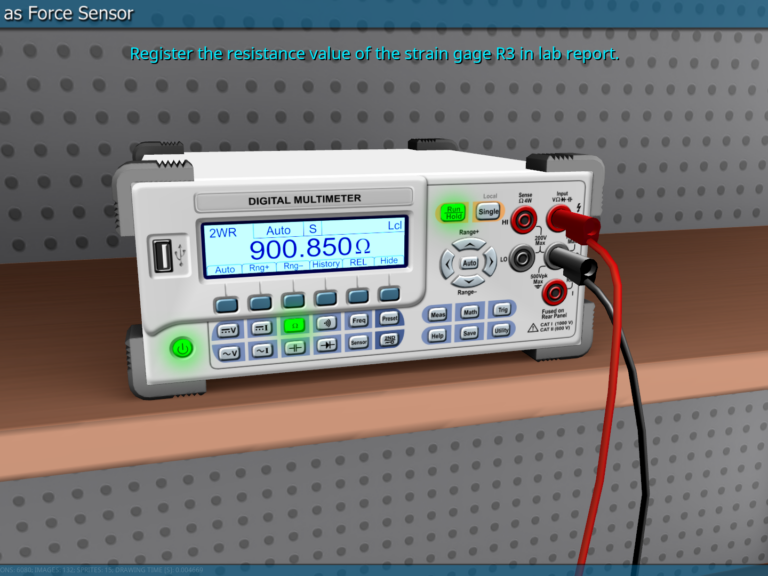
В задачи программного обеспечения входит развитие творческого мышления и профессиональных способностей обучаемых, умения решать вопросы прикладного характера, делать самостоятельные выводы, в виду чего виртуальные лабораторные комплексы и симуляторы должны полностью соответствовать реальному учебному процессу. Приступая к выполнению лабораторного эксперимента, обучаемый должен знать методику исследования и хорошо представлять ход работы, последовательность действий и расчётов. В реальном учебном процессе данную информативную функцию выполняют учебные пособия и брошюры с методическими указаниями. Программные продукты полностью имитируют реальные лаборатории, а методики экспериментов являются неотъемлемой составляющей программных комплексов.
Мультиплатформенность

Представленные программные решения беспрестанно обновляются в унисон с развитием веб-технологий. Одной из приоритетных задач является создание информационно-ёмкого электронного образовательного ресурса – виртуального лабораторного практикума в составе системы дистанционного обучения. Поддержка различных платформ (Windows, MacOS, Linux, Android, iOS, HTML5) способствует более эффективной интеграции программных решений в различные образовательные системы и среды, что позволяет более гибко использовать виртуальные лаборатории в учебном процессе. Программный интерфейс взаимодействия компонентов учебного комплекса ориентирован на работу с совместимыми форматами данных («json», «xml», «csv» и др.).
Области применения программного обеспечения
- Лабораторные занятия студентов в компьютерных классах
- Демонстрационное сопровождение лекций, учебных пособий и практикумов
- Дистанционное обучение с применением телекоммуникаций
- Системы повышения квалификации персонала
- Научные исследования с применением компьютерного моделирования
Общие аспекты эффективности программного обеспечения
- Возможность пронаблюдать процессы, трудноразличимые в реальных условиях без применения дополнительной техники, например, из-за малых размеров наблюдаемых частиц
- Возможность моделирования процессов, протекание которых принципиально невозможно в лабораторных условиях
- Возможность проникновения в тонкости процессов и наблюдения происходящего в другом масштабе времени, что актуально для процессов, протекающих за доли секунды или, напротив, длящихся в течение нескольких лет
- Безопасность – немаловажный плюс использования виртуальных лабораторий в случаях, где идет работа, например, с высокими напряжениями или химическими веществами
Наглядное сравнение различных техник обучения, в том числе имитации реальной деятельности, дает «Конус обучения» профессора государственного университета штата Огайо – Эдгара Дейла (1900-1985):